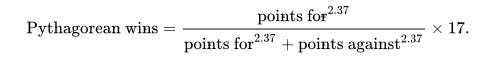What can triangles and baseball analytics tell us about Auburn's 2022 football team?

Yes, you read that correctly.

HC Bryan Harsin (Todd Van Emst/Auburn Athletics)

This is the heart of the college football offseason. Auburn football last played a competitive game a little less than five months ago, and we’re a little under four months away from the start of a new campaign.

At this time of year, most of the attention in American sports is going to the NBA and NHL playoffs. The MLB season is starting to heat up. And, because football is still the king in this country, there’s a whole lot of looking ahead to the fall in the NFL and the college game.

Over the last few weeks, there’s a certain term that seems to be popping up more and more in sports pieces — the Pythagorean expectation. You can find references to it in NBA playoff breakdowns, fantasy football outlooks and a whole lot of baseball analysis.

My first exposure to the Pythagorean expectation in sports came about a decade ago in a piece by Bill Barnwell, formerly of Grantland and now at ESPN. Barnwell used the Pythagorean expectation to preview NFL teams, and it’s a tool he uses in his offseason pieces to this day.

But what is the Pythagorean expectation? You might remember the Pythagorean theorem from math class. (You know, the triangle guy — a^2 + b^2 = c^2.) The Pythagorean theorem for sports is a formula created by Bill James, who is widely known as the father of modern baseball statistics.

James came up with this formula to estimate how many games a baseball team “should have” won in a season, based on the differential of the runs it scored and the runs it allowed. In the early 1990s, Daryl Morey — before he became a famous NBA front office executive — modified James’ formula to fit all major sports, including the NFL.

Here’s the Pythagorean expectation for a 17-game NFL season:

Barnwell breaks down the effectiveness of the Pythagorean expectation in football here:

As an example, let’s take the 2011 Chiefs, who went 7-9 while scoring 212 points and allowing 338. Our formula is 212^2.37 / (212^2.37 + 338^2.37) = 0.248. That’s the Chiefs’ expected winning percentage from their point differential, and if we multiply it by 16 games, we get a total of just 4.0 wins. The Pythagorean theorem suggests that the Chiefs outperformed their true level of performance by three full wins.

Why It Works: Because all wins aren’t created equal. During Kansas City’s three-game winning streak last year, they beat the Raiders 28-0 in a game in which they forced six interceptions. Pretty impressive. A week later, they beat the Chargers 23-20 in overtime during that game in which Philip Rivers fumbled a meaningless snap moments before San Diego could attempt a game-winning field goal. For each of those two performances, Kansas City got the same exact mark on their record: one win. Nobody in his right mind would think that Kansas City looked equally good in both of those games, even if they got the same result. That’s where the “All that matters is the W” argument falls apart. It’s like saying the pass/fail system is just as useful as the traditional grading scale when figuring out how well somebody did in a class.

Barnwell goes on to show that teams’ expected win totals versus their actual win totals in a given season is usually a good indicator of what a team will do the following year. Teams that had one to three fewer actual wins than expected wins in a season improved by an average of at least two wins the next season. Teams that had one to three more wins than expected wins declined by an average of 1.5 to 2.5 wins. In Barnwell’s words, “you can cheat Pythagoras, but not for long.”

The Pythagorean expectation isn’t as prevalent in college football — a sport that has a much larger range of possible opponents and an even smaller sample size than the NFL — but some have used it over the years to project future records. The major outliers usually regress to the mean in a big way the following season.

That brings us to the 2021 Auburn Tigers. What did Pythagoras have to say about Bryan Harsin’s first season on the Plains?

Let’s go back to the formula. Auburn scored 368 points and allowed 283 points in 2021. Plug that in: 368^2.37 / (368^2.37 + 283^2.37) = 0.6507749703.

Multiply that by the 13 games Auburn played, and the Tigers’ expected win total is 8.460074614. Instead of eight or even nine like the expectation suggests, they only won six.